MUSIC & GEOMETRY (The Sacred Geometry Of Music)
“Geometry is knowledge that appears to be produced by human beings, yet whose meaning is totally independent of them.”
– Rudolf Steiner
A note to start this article with:
Perfect geometric shapes only occur when using Equal Temperament. Sonically though the intervals of Equal Tempered instruments/music aren’t perfect (accept for the Octave). They are always a bit sharp or flat in comparison with the Harmonic Series (how sound occurs in nature) and Just Intonation.
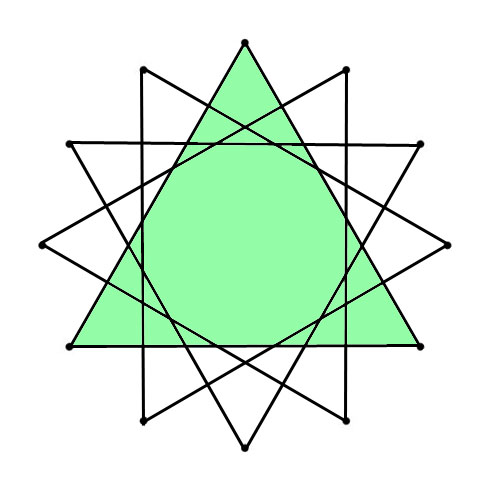
The most harmonious sounding (Just) intervals (the octave excluded) do NOT create perfect symmetrical geometric shapes!
If you “stack” one or more “type” of Just Intervals you will always end up with a spiral!
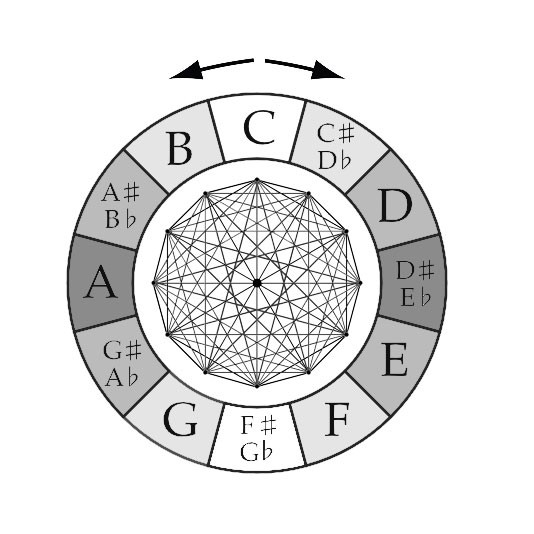
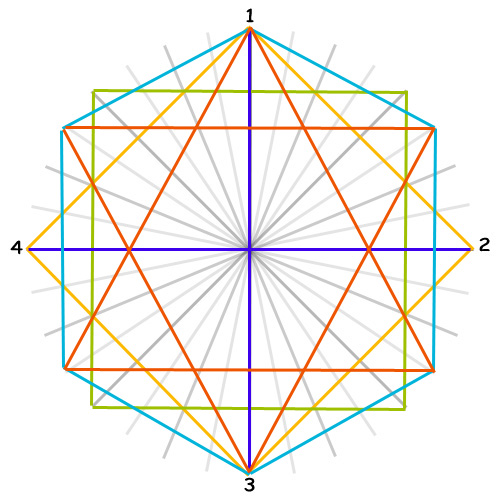
In this article all geometrically perfect shapes (trigone, square, pentagon, et cetera) thus relate to 12-Tone Equal Temperament as do any and all perfect geometrical shapes used on this blog as well as on any other blog, website and book available.
“Music theory has no self-evident foundation in modern mathematics yet the basis of musical sound can be described mathematically (in acoustics) and exhibits “a remarkable array of number properties”.
In its form, rhythm and metre, the pitches of its notes (intervals) and the tempo of its pulse music can be related to the mathematical measurement of time and frequency, offering ready analogies in geometry.”
Now, of course tones and chords are not the same “things” as for example polygons and polygrams. Units like Hertz and Degrees are not the same, they have their own function and use. But in the math behind many “things” there are formulas and ratios (relationships) that are very similar, if not identical. Would it thus be too ‘far-fetched’ to say that the same “rules” apply for many – if not all – things in the universe?
This article will “zoom-in” into geometry in particular.
Over time this article grew so big that the time it took to load started to have a negative effect SEO-wise. I thus decided to split it up in 4 smaller articles: Intervals & Scales, Harmony, Rhythm and Various.